- Five of a kind texas holdem full#
- Five of a kind texas holdem plus#
If you both have three Queens, you have to look at the Pairs to determine the winner. So if you have Q-Q-Q-3-3 and your opponent has J-J-J-2-2, your hand wins because your Three of a Kind (the three Queens) is higher than you opponent's Three of a Kind (the three Jacks).
Five of a kind texas holdem full#
If there are two Full Houses on the table, you have to look at the cards as three of a kind. Full House: Three of a Kind and a Pair.
Five of a kind texas holdem plus#
Four of a Kind: Four cards of one rank, plus any fifth card of any rank or suit. An Ace high straight (A-K-Q-J-10) is called Royal Flush and it is the highest natural hand you can have. Note: Aces can be high or low, but do not wrap around-meaning you can have A-K-Q-J-10, or A-2-3-4-5, but you cannot have K-A-2-3-4. This is the best hand you can have without a wild card (the best “natural” hand).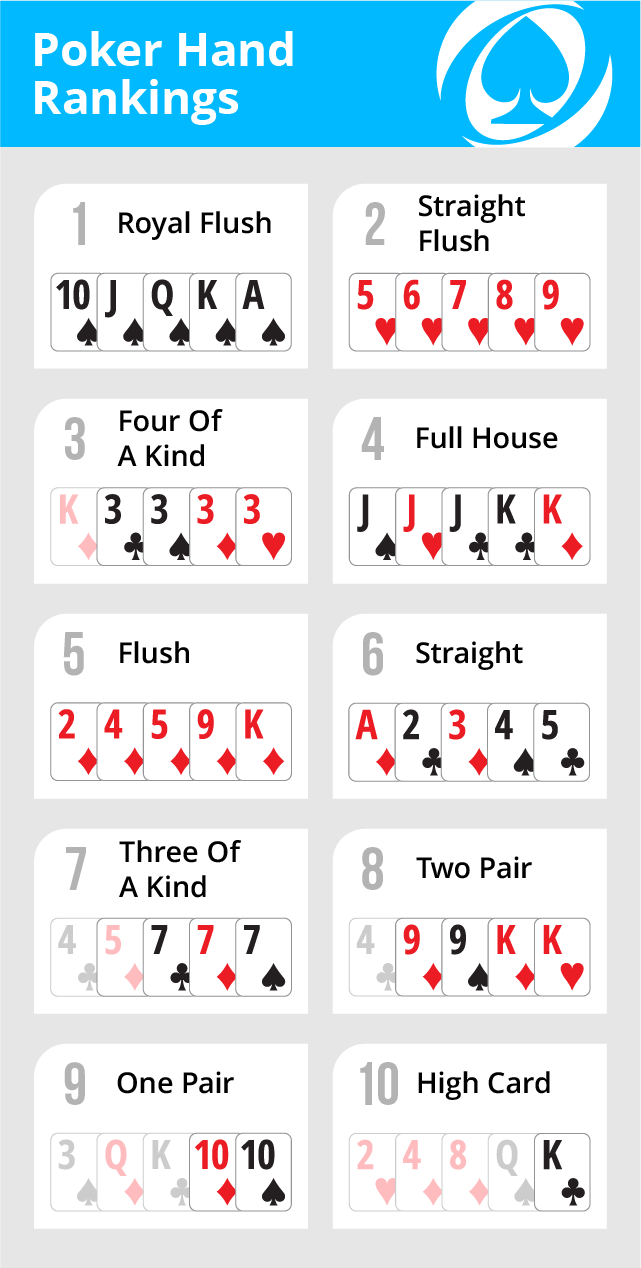 
Straight Flush: Five cards in a sequence in the same suit. Five of a Kind: Four cards of same rank plus a wild card-the highest possible hand. Here are the ranking orders of card combinations: Bluffing relies heavily on your poker face. If your hand is atrocious, but you want to stay in the game, you can try smirking a little throughout the betting process to fool other players into thinking you have a good hand. If your hand is a Royal Flush, you don't want your opponents to know that. Succeeding at a good bluff can depend on the quality of your poker face. You don't want to tip off your opponents to either a good hand or a bad hand. This winds up with $6,589,440-77,220-51,200+600=6,461,620$ hands with three of a kind and nothing higher, in agreement with the Wikipedia page.Poker face refers to keeping a straight face no matter what cards you hold in your hand. There are $40$ straight flushes, $5$ ways to pick the rank that has three of a kind, and $3$ ways to pick the missing suit for $600$ We have deducted the straight flush hands twice, once for the straight and once for the flush. Then there are $5$ ways to pick which card will have the three of a kind and $3$ ways to pick the two other cards, but we have to divide by $3$ for which of the three of a kind was part of the original straight so $10,240\cdot 5 \cdot 3/3=51,200$ hands to deduct. The Wikipedia page shows (assuming that ace low straights count) there are $10,240$ ways to choose the five cards of a straight including straight flushes. Then there are $3$ ways to choose the suit of the flush and $=495$ ways to select the other cards for a total of $77,220$ hands with three of a kind and a flush (which includes the straight flushes).įor straights we will start with the straight. Again there are $13\cdot 4$ ways to get the three of a kind. 
We now need to deduct the number of hands that have a straight or flush. Note this is not many more than the Wikipedia result. Hands with three of a kind and no full house or four of a kind. There are $13$ ways to pick the three of a kind, $4$ ways to pick the three cards of that kind, $48$ acceptable cards for the first odd card, then $44,40,36$ for the following ones, but we have to divide by $4!=24$ for the orders of picking the four odd cards. First we count the number of hands with three of a kind, no four of a kind, and no other pair.
0 kommentar(er)
